Wittgenstein's Manual

From Bayes and Boltzmann to Modern AI
A Framework for the 21st Century Interpretation of the Tractatus

Elizabeth Rohwer

San Diego, CA

erohwer@san.rr.com

ABSTRACT

Interpretations of the Tractatus have been hampered by insufficient understanding of its theoretical underpinnings. Only with the advent of modern AI has the probability theory presupposed by Wittgenstein’s masterpiece been fully fleshed out and applied in practice. That theory has its origins in Boltzmann’s groundbreaking discovery of the nature of statistical inference. Its culmination is a mathematical construct: a fictional common-sense robot able to reason about propositions as human do, invented by Jaynes, one of the founders of modern AI. The paper shows how the robot’s two operations—interpretation and generation, controlled by Bayesian Probability Theory—were foreshadowed in the Tractatus. Jaynes’ robot is a theoretical tool that enables us to calculate the uncertainty at the boundary between the logical and physical space. I claim that, in his treatment of this transition, Wittgenstein extrapolates the foundational law of physics discovered by Boltzmann, to the domain of logic and language.

1. Introduction

Modern AI offers practical solutions to the problem of inductive reasoning. Using algorithms for the optimal processing of incomplete information, AI builds mathematical models of parts of the world. The success of these techniques is attributable to the implementation of a general principle of reasoning that dates back to the 18th century. What is new today is a deeper theoretical understanding of common-sense logic, based on Bayesian Probability Theory (BPT). 

Early AI was entirely rule-based; today, it relies largely on statistics. The availability of big data and powerful computing has given rise to a new type of intelligent application that learns how to perform useful tasks by modifying itself. The commercial success of such applications results from a technique known as ‘machine learning’, which employs a 250-year-old computational rule formulated by Thomas Bayes, a rule that enables learning from statistical data. In brief, a computer program digests the information presented to it in the form of statistical samples reflecting reality, and updates itself by transforming its internal structure. Over time, it becomes better at carrying out the job it is assigned to do. 

This self-improvement occurs through trial and error, one step at a time, guided by another century-old innovation, Ludwig Boltzmann’s breakthrough: a formula for calculating entropy as a measure of uncertainty.

Notably, a Deep Learning Neural Network (DLNN) self-improves by reorganizing its inner structure. The mechanism of how it inflicts on itself those internal structural changes remains hidden. We do not know how a DLNN learns, but we can make it learn to improve its performance. In this regard, it resembles the human mind.

It was the groundbreaking work of the American theoretical physicist E. T. Jaynes, one of the founders of modern AI, that gave us the ability to harness this mysterious mechanism, by bringing together Bayes’s and Boltzmann’s discoveries. Jaynes’ research culminated in a working, powerful probability theory—one that was foreshadowed in Wittgenstein’s Tractatus.

As Hacker (2017) points out, “the deepest commitment of [Wittgenstein’s] first masterwork” was “the distinction between what can be said, and what can only be shown” (210). As he quotes from a letter by Wittgenstein to Bertrand Russell dated August 1919:

Now I’m afraid that you haven’t really got hold of my main contention, to which the whole business of logical prop[osition]s is only a corollary. The main point is the theory of what can be  expressed (gesagt) by propositions—i.e. by language—(and, which comes to the same, what can be thought) and what cannot be expressed by prop[osition]s, but only shown (gezeigt); which, I believe, is the cardinal problem of philosophy. (Hacker 2017, 210)

The other crucial feature of the Tractatus, but one that has received little comment, was, according to Wittgenstein, that the book is “essentially the presentation of a system. And this presentation is extremely compact since I have only recorded in it what—and how it has—really occurred to me.” (quoted in Nordmann 2005, 48).

The framework I shall offer for reading the Tractatus is based on Wittgenstein’s own assessment that it presents a theory that animates a system. The book’s model of the world was inspired by Boltzmann’s statistical thermodynamics, and in so doing it anticipated the key AI computational tool: machine-learning.

2. Wittgenstein’s model of the world as a theoretical instrument

In 1956, just five years after Wittgenstein’s death, E.T. Jaynes wrote a seminal paper titled “How Does the Brain Do Plausible Reasoning?” He had come up with the idea of an intelligent robot that could be used as a theoretical tool to solve the inductive-inference problem. This robot was a mathematical construct designed to reason and behave sensibly under conditions of incomplete information, similarly to the way you and I operate in our everyday lives. It learns how to cope with uncertainty.

The idea was too farfetched for a serious journal of physics, and his paper was rejected. Today, the plausible reasoning—reasoning that takes uncertainty into account—has been fully developed. The robot’s theory, BPT, has been known for a long time, but Jaynes saw it in a new light. The robotic contraption he envisioned contributes to the correct interpretation of probability as common-sense reasoning learned from statistical data. Wittgenstein, who had been trained as an engineer, was proficient in thermodynamics and had an aeronautical patent to his name, was able to foresee such an application of BPT. His model of the world, which was designed to facilitate his philosophical investigation into logic and language, foreshadowed Jaynes’s intelligent robot.

Jaynes had the ingenuity to turn around the focus of the question as usually posed: “Instead of asking, ‘How can we build a mathematical model of human common sense?’ let us ask, ‘How could we build a machine which would carry out useful plausible reasoning, following clearly defined principles expressing an idealized common sense?’” (2003, 8; my emphases). Those were the very principles that Wittgenstein had been seeking, following attempts by his predecessors—Aristotle, Gottlob Frege and Bertrand Russell—to delink logic from language and confine it to formal expression. 

From the point of view of modern AI, Wittgenstein’s book is concerned not with the abstract construction of an ideal language, as Russell wrote in its introduction, but rather with the procedural rules that would enable an intelligent device to reason about propositions: generating and interpreting them in the way you and I do. Against this backdrop, the Tractatus can be seen as an engineering project that features a philosophical system grounded in a model of the world that is a precursor of AI’s universal model of common sense.

3. The Tractatus’ system and story

The Tractatus, Wittgenstein states in the preface, is “not a textbook” (TLP, 3). With its sparse prose and strict tree-like structure—a numbered set of statements with subordinate branches—it reads like a technical manual. It details the operations of a system, Jaynes’s robot ancestor, explaining how it could acquire the skill of linguistic communication. In order to do so, it repeatedly performs generation and interpretation of propositions. It learns language by using it. 

There are two processes, operating on different time scales that constitute Wittgenstein’s model:

1. 1. Language learning—a process that accumulates statistics over an extended period of time.
2. 2. Language use—an instance of linguistic transmission of meaning from a speaker to a listener.

The Tractatus tells the story of how they interconnect. 

Let us picture their time-dependent relation as freight trains with locked consignments of cargo (meaning) traversing a gigantic rail network. Similarly, strings of words crisscross between same-language speakers in a formidable web of transactions of meaning in an infinite span over space and time. The network traffic provides the statistics of language use. Statistics enables learning of meaning. The Tractatus explores the hustle and bustle happening at the train station’s docks where each train’s cargo gets loaded or unloaded and the goods put to use by the listener-speaker train-station master. Needless to say, a train loaded today can not deliver its shipment yesterday—a constraint imposed by the arrow of time that establishes the order in speech.

The main activity in the network of linguistic exchanges of meaning is disambiguation which is a technical term for clarification of meaning. To disambiguate is to remove uncertainty of meaning from an ambiguous linguistic unit (word, sentence or phrase). Uncertainty and clarification of meaning, their interplay, is what the Tractatus reveals. It tells what is done with meaning—loaded, transported, unloaded —not what meaning is. It defines meaning through the operations performed on it, lists the critical stages in the process and shows how they interoperate. By both its form and content, the Tractatus is an operational manual for a system designed to disambiguate.

Its structure is distributed over space and time and has an infinite number of listener-speaker nodes. Its building block is one instance of linguistic communication: a freight train transporting a locked consignment of meaning. The train’s cargo is locked in at the departing train station and unlocked after the train has arrived at its destination. The shipment seems secured, but it is not. Its locking and unlocking are not done as one would expect. Unlike the lock on a suitcase whose key the traveling owner uses before and after her train journey, the word-train is locked by one train-station master (the speaker) and unlocked by another (the listener). The problem is that their keys never quite match (Figure 1.). The Tractatus’ hard to grasp story is about the mystery of the lock. How would the key of the listener open the lock closed by the speaker? How does the listener understands the speaker’s words?

Fig.1 How a sentence differs from a proposition

The meaning a speaker encrypts in her string of words is not exactly the meaning her listener gets out of them. Something happens to it along the way. An unwarranted transformation occurs. The train that departs and arrives is the same; its freight wagons stay locked; the string of words is preserved. A sentence does not change. And, yet, the train’s cargo at the loading and unloading end is inevitably different. This discrepancy is addressed by Wittgenstein’s theory of what can be expressed by propositions which is the main point of the Tractatus. 

Wittgenstein’s masterpiece is a philosophical investigation into how a fixed sequence of words, shown as a speech audio signal in Figure.1, transports intangible meaning from speaker to listener, what happens to the train’s cargo, and who is the culprit behind its undesirable, yet unavoidable change. The discrepancy has been mathematically pinned down by Boltzmann who applied statistics (the theory of probability) to the study of the phenomena at the boundary between inner and outer.

4. How does a proposition differ from a sentence?

Wittgenstein tells a mathematically tenable story whose theoretical underpinnings originated in Thomas Bayes’s 18th-century interpretation of probability, and which draws inspiration from the 19th-century’s revolutionary discovery in thermodynamics: Boltzmann’s entropy calculation as a measure of disorder. It is the story of a speaker–listener system, the statistical theory that sets it in motion, and a mysterious entity that drives the action and is thus the protagonist: The Proposition. Its character arc begins with the notion of a proposition shown in Figure 1, culminates in the proposition’s general form (TLP 6), and ends with the coda of TLP 7: a clearly stated, correctly-ordered string of words better communicates meaning. 

Put it differently, the Tractatus outlines a generalization process that is internal and is then expressed externally via ordered words. The book’s motto, borrowed from the Austrian writer Ferdinand Kürnberger, sums up the three components of the system set in motion by it: internal state, input, and output.  “Motto: …and everything you know, not just heard rumbling and roaring, can be said in three words. Kürnberger” (TLP, 1, emphasis in original). A motto prepares the reader for what to expect when reading the book. In this case: an explanation of how we generalize using linguistic transactions. Thus, Wittgenstein’s book is about a speaker-listener system, the statistical theory that sets it in motion and a mysterious entity – The Proposition – which steers the action.

The proposition is the principle character of Wittgenstein’s story. It does the saying. How it does this—how it happens that, as 5.542 has it, “‘p’ says p”—is the mystery of the story. The notion of the proposition as a non-consistent unit of meaning, one plagued by uncertainty, is crucial to the answer. It has been suggested that Wittgenstein used the German word Satz as a working title for his manuscript (Hacker 2017, 211). The term is variously translated as ‘proposition’ or ‘sentence’, but also as ‘statement’, ‘assertion’, ‘utterance’, ‘remark’, and ‘what was said’. The ambiguity contributes to the difficulty of understanding Wittgenstein’s story.

As Figure 1 shows, a proposition differs from a sentence. A sentence is physical; a proposition is not. It manifests itself through its dual projections into and out of reality. The sentence is the train that transports word-locked meaning. The proposition is an abstraction developed as an analytical tool to connect the meaning that the speaker encrypts in her words with the meaning decrypted by the listener. That the encryption key of the speaker does not quite match the decryption key that her listener has—is the foundational premise of Wittgenstein’s story.

5. The bidirectional link between logical and physical space 

To explain the discrepancy, Wittgenstein develops a theory—a nascent version of BPT—which is central to his book. It addresses the problem of the inner–outer relation through the dual role of the proposition in the transmission of meaning. Figures 2 and 3 illustrate the approach, offering a framework for a uniquely coherent reading of the Tractatus that renders it consistent with the author’s later philosophy. These two figures present two complementary viewpoints of Wittgenstein’s logical space in relation to the physical space. Both when juxtaposed and when considered as a repeated sequence, they illustrate how Wittgenstein’s model of the world operates, powered by the theory of what can be expressed in propositions. 

Jaynes’s robot, whose task it is to generate and interpret propositions, validates this approach. Its ability to impersonate a human communicating with language renders it intelligent. In the same way, the Tractatus depicts how common-sense reasoning in idealized form—as if done by an intelligent robot—enables the traffic of meaning to move through the language communication network.

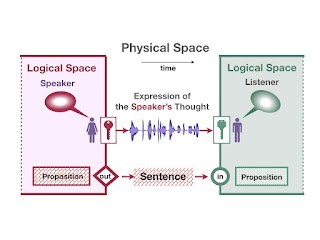Fig.2  AI Framework PART I - Speaker and Listener are two different people

In Figure 2, the logical space is split in two. The proposition undergoes a twofold transformation: from the speaker’s thought, through the physical expression of that thought as a string of words (the propositional sign), into the listener’s thought. The two conversions happen at two different points in space and time. They correspond to the two reciprocal activities of speaker and listener: the loading and unloading of cargo. The meaning of the speaker’s proposition—what the sentence transports—is shown as a red tile. The meaning that the listener receives has been altered. It has the same tile-like texture, but has been altered (reduced in size), and it is green because it is inside the listener’s logical space. The disparity in color and size indicates that uncertainty has been at work. Always present in the physical space it afflicts the transmission of meaning.

Fig.3 AI Framework PART II - An agent Speaks and Listens 

Figure 3 shows Jaynes’s inversion. This time, the two conversions are carried out by the same station master (Jaynes’s robot), whose logical space is an integrated whole. What makes it whole is the generalization process, summed up poetically in the motto and analytically with the logical formula of TLP 6. The logical space remains hidden, but it is not closed. It has an entry and an exit through which the robot communicates by sending and receiving linguistic units of meaning. The bidirectional connection between the logical space and the physical space enables the robot to learn how to use language. Learned language and a shared physical space are thus prerequisites for the transmission of meaning.

6. Interpretation and generation—the essential constituents of machine learning

Jaynes’ fictional robot is a node in the distributed network for the transmission of meaning. It uses the same key to unlock the cargo of an arriving train and to lock that of a departing one. It learns how to perform its assignment through trial and error from the statistics of the network traffic, (i.e., from the language samples to which it has been exposed). Those are the trains that had stopped at its station. Notably, they are but a fraction of the infinite network’s traffic. The robot fine-tunes its key on them until it can unlock the majority of consignments of meaning locked by many different speakers at different points in time. Its master key works in both directions. The unlocking corresponds to the interpretation, the locking – to the generation of speech.

Overtime, the robot becomes an intelligent communication device, a linguistic agent capable of interacting with humans by receiving and sending strings of words through the Physical Space. It learns to reliably perform its assignment, acquires commonsense and attains coherence. For this to happen, its training has to follow two simple qualitative rules, today known as the Cox–Jaynes axioms. They render the strings of words that the robot generates, internally consistent and in sync with the external messages from the other participants in the communication exchange. The robot learns how to understand others and make itself understood. It learns language gradually, over time, by using it.

The Tractatus’ system operates on the same conceptual scheme. Its picture theory tackles the process of language acquisition across time. Its theory of logic addresses how the interpretation and generation of speech are internally linked. Both are parts of a nascent version of today’s Bayesian Probability Theory which is used to program the neural networks that animate Jaynes’ fictional robots. The theory connects the generation with the interpretation process through the extended notion of logic. Plausible logic, or the logic of uncertainty, enables the construction of a universal, unique model of commonsense reasoning. Foretelling how such a model works in the field of language communication is Wittgenstein’s crowning achievement.

Like Jaynes’ robot, the Tractatus’ system operates on the extended notion of logic defined by the language-independent rules of common sense that govern the logical space (Figure 3). This goes a step further from the formal logic expressed in language and captured by the symbolism of Frege and Russell that takes effect in the physical space (Figure 2). The difference is akin to the difference between the Bayesian (subjective) and the frequentist (objective) approach to statistics. Thus, the decoupling of logic from language is a result of the bidirectional link between the logical and the physical space. The Tractatus depicts the two reciprocal processes corresponding to Jaynes’ robot two tasks: interpretation and generation of speech.

7. The big picture

Figure 2 and 3 are conceptually linked: first, as an instance of a transaction of meaning and second, as a repeated sequence in the language communication network. Together, they provide a synoptic view of Wittgenstein’s system. The framework has three parts:

1. I. Part I shows the arrow of time running through the Physical Space (Figure 2):

    Logical Space → Physical Space → Logical Space

The generative side of the speaker is connected externally to the interpretative side of the listener, via physical space.

1. II. Part II shows the arrow of time piercing the Logical Space entering it and exiting. (Figure 3):

    Physical Space → Logical Space → Physical Space 

Here, the interpretive and generative sides are connected internally through thought—the intangible human ability to generalize (i.e., to make inferences from incomplete information).

1. III. Part III shows the path of communication between multiple people (Figure 4):

…→ Logical Space → Physical Space → Logical Space → Physical Space → Logical Space → Physical Space →….

The pattern remains the same across space and time regardless of the number of participants in the network. Notably, each participant is both a speaker and a listener.

Fig.4 AI Framework PART III - The statistical dimension, repetitions over time 

A proposition is generated in the speaker’s logical space, exists as sounds in physical space, and is interpreted by the listener’s logical space. The Tractatus’s symmetrical structure shows the transition: In TLP 1,2,3, a thought becomes a proposition; TLP 4,5,6 a proposition becomes a thought. Notably, the analyzed proposition connects two thoughts from two different logical spaces: the source’s and the receiver’s.

The Tractatus depicts the transition inner — outer — inner. The passage through physical reality is accompanied with an informational loss when the external vehicle is the sentence. This loss creates the uncertainty in the transmission of meaning.

At the same time both the hearer and the speaker’s logical spaces function in the same way. Every human can both hear and speak. That’s the Tractatus’ summersault trick: it describes my input / output channels and how they connect to yours. Note the crisscross: my output connects to your input. My thought becomes a proposition that in turn becomes a similar thought of yours.

8. Uncertainty, ignorance, lack—the analogy with Wittgenstein’s silence

We reason about propositions with uncertainty. Often, it is not clear whether a complex proposition is true or false. A materialized proposition as a sentence becomes public in the physical space. It might seem true to me, and false to you. How true? And how false? We both are unsure (or sure) to a different degree. The Bayesian interpretation of probability as a degree of belief extends the scope of logic beyond the Aristotelian two-valued deductive reasoning. The ensuing theory is a mathematical framework for dealing with uncertainty. It narrows the uncertainty when Jaynes’ robot has to carry out a clear-cut task. The robot takes into account all the information available for the task and also the information that’s lacking.

Paradoxically, that second part—the robot acknowledging its ignorance—is what made the AI model of common-sense reasoning applicable to so many different tasks. In a 1918 letter to Engelmann, Wittgenstein illustrates its significance, albeit in a different (self-awareness) context. “I am now slightly more decent,” he wrote. “By this, I only mean that I am slightly clearer in my own mind about my lack of decency” (1967, 11). Here is the algorithm for an AI ‘decency’ machine as Wittgenstein calls it. Task: becoming decent. Result: being more decent, which is an upgrade of (an improvement on) my state of decency. Means: acknowledging my lack of decency. Bayes’s inverse probability rule does the upgrade; Boltzmann’s maximum entropy formula, calculating the lack, guides its direction. Once more, the structure of the Tractatus conceptually reflects that scheme:

1. TLP 1, 2, 3 and TLP 4, 5, 6 describe how the robot learns and operates.
2. TLP 7 signals the lack, (i.e., the importance of what is missing). “What one cannot speak of, one must be silent about.” Without taking into account its ignorance, the robot cannot learn to operate. This is a theoretical must. It is in this way, that the TLP 7 remark is vital.

That is why the Tractatus is bookended by that observation. It had already been stressed in the preface: “The whole sense of the book might be summed up in the following words: what can be said at all, can be said clearly [conveying meaning], and what we cannot talk about [because talking about it will cause confusion, increase uncertainty] we must pass over in silence.” Note how emphatic Wittgenstein is. It is not mere advice; it is an order. Everyone disobeying his dictum will whirl around the drain and sink others with him. That is a mathematical certainty. The ethical purpose of the Tractatus is to alert us to our own ignorance, urging us to continuously ‘upgrade’ in order to do better coping with uncertainty. 

Consider, in tandem with this, another oft-quoted remark by Wittgenstein: “My work consists of two parts: the one presented here plus all that I have not written. And it is precisely this second part that is the important one. […] I have managed in my book to put everything firmly into place by being silent about it.” (Engelmann, 1967, 143) This reaffirms the understanding of uncertainty that Jaynes developed. There is a mathematical proof that Wittgenstein’s silence maxims are not a trivial matter.

10. Jaynes’s silence: The historical links to Boltzmann, de Finetti, and Ramsey

Jaynes’s contribution to science was to bring together two known mathematical tools for reasoning in conditions of uncertainty, namely Bayes’s inverse probability and Boltzmann’s maximum entropy. Both formulae were used by late 19th-century physicists, but their workings were not well understood at the time. We owe their correct interpretation to Jaynes. He reformulated Boltzmann’s statistical mechanics as a problem of inference. But Jaynes’s novel understanding of the statistical nature of inference had also been foreshadowed in the Tractatus. Wittgenstein’s work as a young engineer, with kites, balloons, and turbo-propellers, had established the technical background in mechanics and thermodynamics that would shape his thinking in the same way as Jaynes’s.

Wittgenstein explicitly acknowledged Boltzmann’s influence on his own thought. (C&V, 19) Boltzmann had discovered the mathematical link between the inner, unknown micro-state of an ideal gas in equilibrium and its outer macro-state, whose physical characteristics can be measured (volume, temperature, pressure). The statistical properties of the two spaces, the hidden (inner) and the accessible (outer), are connected through Boltzmann’s entropy formula. Similarly, the Tractatus explores the connection between the hidden (inner) logical space and the accessible (outer) physical space (Figure 3). Thought is hidden; its expression with a propositional sign, whether that be written or spoken, is perceptible, real, and available for analysis. The two are connected by the statistical properties of matter.

At the time, Boltzmann himself did not have a theoretical explanation for his discovery. His formula as well as Bayes’s rule are empirical discoveries that worked great in practice. Nobody knew why. Boltzmann’s breakthrough was so much at odds with the established way of thinking that he, disheartened by his detractors’ attacks, took his own life in 1906, the year Wittgenstein had planned to study with him. When statistical mechanics led to the foundation of quantum mechanics, the validity of Boltzmann’s approach was confirmed. Today, Boltzmann’s entropy formula is engraved on his tombstone.

Wittgenstein’s prescience has a historical link with the research efforts of Frank Ramsey and the Italian scholar Bruno de Finetti, in the 1930s. Their simultaneous and independent inquiries into ‘subjective probabilities’ had paved the way for Jaynes’s robot. De Finetti came up with the subjective YOU concept. His use of capital letters denotes an idealized agent—the grandfather of Jaynes’s robot’s. Ramsey’s notions of a ‘utility function’ and ‘Dutch bet’ are precursors of today’s ‘operational subjectivity’ approach. The continuation of de Finetti’s work led to today’s machine-learning algorithms that self-improve, optimizing their own performance.

Wittgenstein’s treatment of the inner–outer transition is substantiated by Jaynes, whose statement on silence stresses the importance of Boltzmann’s discovery: “At first glance it seems idle and trivial that we should have to do all this in order to learn HOW TO SAY NOTHING [my emphasis]”. And he continues:

The important point, however, is that we have here found a consistent way of saying nothing in a new language: the language of probability theory. The triviality fades away entirely when we notice that the problem of inferring the macroscopic properties of matter [measured in empirical reality] from the laws of atomic physics [the matter’s hidden states] is exactly of the type we are considering [reasoning with propositions]. All of thermodynamics, including the prediction of every experimentally reproducible feature of irreversible processes, is contained in the above solution [i.e., the probability theory, notably the transmission of meaning with a sentence is an irreversible process]. (Jaynes 1957, 22, emphasis in original)

Jaynes’s new ‘language: the language of probability theory’, which was anticipated in the Tractatus, is mainstream today.

11. Wittgenstein’s crowning achievement, theoretically proven

Wittgenstein was hot on the trail: “I saw something from far away and in a very indefinite manner, and I wanted to elicit from it as much as possible” (quoted in McGinn, 2006, p. X) Events (propositions), order, and time—the statistical connection between the observable properties of matter and their corresponding hidden states—is the thread that connects the Tractatus with Wittgenstein’s later philosophy and brings forth the consistency of his thinking. Two days before his death in 1951, he wrote: “We might speak of fundamental principles of human inquiry” (OC, 671).

The timing of that remark was not coincidental. The uncovering of the BPT principles had begun in the preceding decade. In 1946, Richard Cox formulated its axioms (the Cox–Jaynes axioms). Claude Shanon’s 1948 communication theory, to everyone’s surprise, rediscovered Boltzmann’s entropy formula as a measure of the loss in an information transmission channel, confirming the universality of the approach. It became a stepping-stone for Jaynes’s development of BPT. Jaynes demonstrated why his robot’s ignorance equals the loss of information in the communication (speaker-to-listener) channel.

Crucially, BPT provides a rigorous way by which to infer backwards, switching the places of cause and effect. The inversion has been a source of confusion because it changes the meaning of probability from the ‘probability of things’ (objective) to our ‘beliefs about things’ (subjective). Wittgenstein had the right intuition and in TLP 5 traces the premises, axioms, and applicability of BPT to the domain of logic and language.

The most important breakthrough discovery of BPT is its uniqueness theorem. It corroborates

Wittgenstein’s claim about his book’s remarkable achievement: “[T]he truth of the thoughts that are here communicated seems to me unassailable and definitive. I therefore believe myself to have found, on all essential points, the final solution of the problems”. (TLP, 4) He did. The uniqueness theorem proves that there is no better way to do rational thinking than the one based on the principles of BPT. There is a single set of rules for uncertain reasoning that is consistent and objective and, according to Jaynes, so powerful that several laws of physics can be derived from them. The key to the uniqueness theorem is anticipated in 5.1: “…truth functions arranged in series.” Preserving the order is at the heart of BPT power and magic. The rest of section TLP 5 comes to light when the role of language in communication is technically examined.

12. Shannon’s communications theory gives credence to Wittgenstein’s wishes for his readers 

In the preface, Wittgenstein defines the aim of his book and two prerequisites. In the context of Shannon’s communication theory, they seem broadly analogous to the properties of the source, the channel and the receiver that are necessary for a successful message transmission. 

When I generate a proposition (as per TLP 1,2,3) and YOU interpret what I am saying (TLP 4,5,6), we communicate: I’m the source; you are the receiver; the physical reality is the channel. Theoretically, the source and the receiver have to share a codebook, and the channel has to be able to transmit the message encoded by it. If Wittgenstein is the source and his book a message to me, his reader, in order to understand what he is telling me, I have to have had thoughts similar to his. Figuratively speaking, the same or similar thoughts establish a common codebook prior to the message exchange. Hence, Wittgenstein’s cautionary presupposition about the preparedness of his reader from the preface’s opening statement. “Perhaps this book will be understood only by someone who has himself already had the thoughts that are expressed in it—or at least similar thoughts.” (TLP, 3)

His other prerequisite requires the source: “To say clearly what can be said…” (TLP, 3) Wittgenstein’s lapidary writing does that. He had applied the requirement to himself as a writer. The Tractatus cannot be more precise and clear. It is the most beautiful book, but its message is rooted in the mathematical apparatus of a theory which was developed a century later. To get it, its readers have to step up to the plate and familiarize themselves with the key principles of BPT. 

The circumscription of the source and receiver leads to more effective communication, i.e. to less loss of information in the message transmission—in the language of Shanon’s communication theory. The demands on the writer and reader, Wittgenstein writes about, are a reformulation of the same condition. Its necessity becomes obvious when the machine learning techniques that teach Jaynes’ robot to reason are examined.

13. Boltzmann’s entropy clarifies Wittgenstein’s goal

For the communication to happen, one more condition has to be met. It throws light on the aim Wittgenstein set for his book: “To draw a limit to the expression of thoughts in language.” (TLP 3) In communication theory, Boltzmann’s formula for calculating entropy acquires a broader interpretation. It expresses the absolute mathematical limit for intelligible message transmission. For humans to understand each other, the information content of the messages we exchange has to obey that theoretical limit. That limit exists, it is a number, a measure of the capacity of the communication channel when YOU and I talk. 

Conceptually, entropy is similar in an inverse way to the output of a scale, thermometer, clock, ruler, etc. All those are communication devices. They help us communicate to each other the measurable properties of physical reality: weight, temperature, time, length, etc. They coordinate our actions and optimize their results. Likewise, language is a communication device. It helps us communicate meaning, which cannot be measured, but its opposite—the lack of meaning—can, with Boltzmann’s entropy formula.

A few decades prior to Shanon’s discovery, Wittgenstein was seeking the limit of thought communicated in language. He was trying to find the connection between the meaning of a thought (hidden) and the meaning transferred by a meaningful string of words through physical reality which is measurable through the loss in the communication exchange. He establishes their relationship through the notions of form, pictorial form, logical form, and the general propositional form. They are aligned through the statistical properties of matter. Their progressive transformation goes from my logical space (invisible thought of the source), through physical space (matter’s measurable properties), to YOUR logical space, (invisible thought of the receiver).

Jaynes’s breakthrough discovery is that the entropy formula can be applied twice:

1. To measure the information loss between the source and the receiver in Shanon’s sense;
2. To connect matter’s internal, hidden states with its public, empirical, macro properties – Boltzmann’s original application.

14. The structure of the Tractatus 

Through the structure of the Tractatus Wittgenstein coveys both. He combines Boltzmann’s entropy as a measure of my ignorance and Shannon’s entropy as a measure of the communication loss of my message to YOU, to express the intrinsic uncertainty of the world. That’s my world, YOUR world and the empirical reality that connects us—combined. To attain his objective, he expresses the limit of thought through the symmetry of the six key propositions and the progression of the notion of form.

Wittgenstein’s formula for the general propositional form, the crown jewel of his book, can be clarified in terms of choice, meaning, and entropy—the probabilistic measure of uncertainty. Those are the theoretical constituents of a communication exchange. TLP 1, 2, 3, 4, 5 show how TLP 6 is arrived at through the progression of the notion of form. The same six key TLP remarks outline how Jayne’s robot (I) learns and once trained, (II) operates. “Once trained” holds the key.

A parallel can be drawn between an AI algorithm for machine learning and TLP sections 1,2,3 and 4,5,6 seen as the two parts of a process repeated many times in a loop. One cycle around the loop is one step in the robot’s training procedure. Over time, the robot becomes intelligent and acquires a skill. It learns by itself how to materialize form. With each consecutive step, repeated time and again, it builds itself. It gets better at consolidating the form’s invisible structure and materializing it as a result that eventually becomes good enough to be gainfully used. Training takes time.

Humans materialize form into a sequence of ordered words. We too learn the language skill incrementally, over many time steps, starting age two through trial and error. We listen and speak in a great many loops. The process interpolates twice: over time and over a distributed network of people generating many diverse samples of successful language communications. 

To convey it, Wittgenstein details the workings of one such loop, employs a writing technique, and develops a major theoretical innovation: 

1.) The Tractatus six key sections are organized in two symmetrical parts. They connect and then run (project) in opposite directions: out and in. TLP 1,2,3 (out) mirrors TLP 4,5,6 (in). The symmetry is V-shaped. 

2.) At the same time, the TLP 1,2,3,4,5,6 linear sequence depicts the progression of the notion of form. Its transformation goes from: form as possibility of structure, through pictorial and logical form, to the general propositional form (materialized structure expressed in ordered words). The movement of the text is simultaneously V-shaped and linear. Its already complex, tree-shaped construction carries two extra functions.

3.) What holds everything together is Wittgenstein’s Bayesian treatment of the statistical properties of matter—an innovation miles ahead of its time. 

How Jaynes’ robot interprets a proposition conceptually mirrors TLP 4,5,6. While its training takes time (many loops in and out of physical reality), its operation is instant. This is an idealized distinction. The point is that time, a physical property of matter, plays no role in the interpretation process. “6.1263 In logic, process and result are equivalent. (Hence the absence of surprise.)” Logic is about consistency – BPT postulates.

14. The connection with modern AI

Jaynes’ robot is both an active agent that works on itself while learning and an ordinary machine, when operating. Interestingly, there is no uncontroversial AI technique that can fully decipher how the robot’s internals work. Something stays hidden. The neural networks that model its reasoning cannot be reverse-engineered the way a standard computer program can. Their ability to learn by themselves to spot patterns without external structural information is key to today’s AI success. 

The AI algorithms extricate form. Form is a hypothetical structure, “a possibility of structure” (TLP 2.033) It is intangible, hidden—an unrealized possibility. Structure is tangible, real – a recognizable pattern. The form is possible—its corresponding structure probable. The AI neural network’s magic bridges the metaphysical divide, turns the possible into probable. We do not how they do it, but we can make them do it. 

The Deep Learning Neural Networks (DLNN) are getting increasingly better at bringing into useful existence sophisticated, intangible forms. They do that by sewing stitches over the possible–probable gap, known also as the inner–outer divide, or mind–reality split, or in Tractarian speak, the boundary separating the logical space from the physical space. (The physical space has a tangible time component, the logical space doesn’t.) Today’s increased computer power, advanced hardware designs and big data allow for the stitches to be done in huge numbers. But the basic principles—how to make a stitch over the gap and be able to keep stitching—were known in the 19th century. 

Bayes’ Inverse Probability is used to update Jaynes’ robot with new information, one step at a time—the stitch. Boltzmann’s Max Entropy Inference guides the update—in charge of the embroidery. Wittgenstein was familiar with both principles. His book is a work of a brilliant engineer, someone who at the age of ten had constructed a “functioning model of a sewing machine out of bits of wood and wire”. (McGuinness, 1988 )

Parallels with BPT can be traced throughout Wittgenstein’s writings. They bring to light the cohesiveness of his oeuvre. It holds up to science—that’s the source of its philosophical strength. For instance:

TLP 5.152 exemplifies Bayesian inversion: “If p follows from q, then the proposition ‘q’ gives to the proposition ‘p’ the probability 1.” 

TLP 5.155 confirms Wittgenstein’s Bayesian thinking. “The minimal unit for a probability proposition is this: The circumstances—of which I have no further knowledge—give such-and-such a degree of probability to the occurrence of a particular event” (my emphasis).

TLP 1.56 makes the connection with uncertainty: “We use probability only in default of certainty—if our knowledge of a fact is not indeed complete, but we do know something about its form” (emphasis in original).

15. Conclusion

This paper has outlined a framework for reading the Tractatus from a technical point of view, steeped in Wittgenstein’s own assessment that his book is “essentially the presentation of a system,” (quoted in Nordman 2005, 48) and that its “main point is the theory of what can be expressed by propositions” (Hacker 2017, 210). It shows that Wittgenstein’s system is conceptually similar to Jaynes’s common-sense robot, and his theory is a nascent version of modern BPT.

This new approach to the Tractatus can be summarized as follows. Meaning encoded in strings of words that follow a strictly pre-established order is transported through physical space from speakers to listeners. How those strings are generated and interpreted in the two logical spaces they connect is the subject of Wittgenstein’s book. How order, imposed by and manifested in language, gets created at the boundary between logical and physical space is the story question. The Tractatus tells us what happens between those spaces: the transformations of the proposition from intangible to real and then back to intangible. Its story is supported by Bayes’s and Boltzmann’s monumental discoveries about the statistical relationships that govern the transition between the hidden inner, corresponding to Wittgenstein’s logical space, and the measurable material outer, known as empirical reality, or physical space. It is the story of their bidirectional connection, which Jaynes had articulated.

My goal has been to equip the reader with the necessary technical information to become “someone who has himself already had the thoughts that are expressed in [the Tractatus]—or at least similar thoughts,” which was Wittgenstein’s prerequisite for understanding his book. My hope is that against this backdrop Wittgenstein’s masterpiece would “give pleasure” not just to the “one person who read and understood it,”(TLP, 3) but to most of its 21^st-century tech-savvy readers. Because no profit grows where is no pleasure taken.

References

Hacker, P. M. S. 2017. “Metaphysics: From Ineffability to Normativity.” In A Companion to Wittgenstein. Edited by H.-J. Glock and J. Hyman. Oxford: Wiley-Blackwell.

Nordmann, Alfred. 2005. Wittgenstein’s Tractatus. Cambridge: Cambridge University Press.

Jaynes, E. T. 2003. Probability Theory: The Logic of Science. Cambridge: Cambridge University Press.

Jaynes, E. T. 1957. “How Does the Brain do Plausible Reasoning?” In Maximum-Entropy and Bayesian Methods in Science and Engineering. Edited by G. J. Erickson and C. R. Smith, 1–24. Fundamental Theories of Physics, vol. 31–32. Dordrecht: Springer.

McGuinness, B. 1988. Wittgenstein: a Life: Young Ludwig. Berkely: The University of California Press.

Wittgenstein, Ludwig. 1910, Improvements in Propellers Applicable for Aerial Machines. GB Patent 191027087A, filed November 22, 1910, and issued August 17, 1911.

Wittgenstein, Ludwig. On Certainty (OC).

Wittgenstein, Ludwig. Culture and Value (C&V).

Wittgenstein, Ludwig. Tractatus Logico-Philosophicus, Translated by D.F. Pears and B.F. McGuinness, Rutledge & Kegan Paul (TLP).